पूर्णांक | Integers

पूर्णांकों में धनात्मक संख्याएँ, ऋणात्मक संख्याएँ और शून्य शामिल हैं। ‘पूर्णांक’ एक लैटिन शब्द है जिसका अर्थ है ‘संपूर्ण’ या ‘अक्षुण्ण’। इसका मतलब है कि पूर्णांकों में भिन्न या दशमलव शामिल नहीं होते हैं।

पूर्णांकों की परिभाषा

पूर्णांक वे संख्याएँ होती हैं जो न तो दशमलव होती हैं और न ही अंश। ये संख्याएँ शून्य, सकारात्मक और नकारात्मक हो सकती हैं।

पूर्णांकों के उदाहरण: – 1, -15, 6, 17.

प्रतीक

पूर्णांकों को ‘Z‘ द्वारा दर्शाया जाता है। 

Z= (……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,……)

पूर्णांकों की श्रेणियाँ

• सकारात्मक पूर्णांक: ये संख्याएँ 1, 2, 3, 4, आदि के रूप में होती हैं और ये शून्य से बड़ी होती हैं।
• नकारात्मक पूर्णांक: ये संख्याएँ -1, -2, -3, -4, आदि के रूप में होती हैं और ये शून्य से छोटी होती हैं।
• शून्य (0): शून्य एक विशेष पूर्णांक है जो न तो सकारात्मक है और न ही नकारात्मक।

संख्या रेखा

संख्या रेखा पर पूर्णांकों को दर्शाने से उनकी स्थिति और क्रम को स्पष्ट किया जा सकता है। संख्या रेखा पर पूर्णांकों को इस प्रकार दर्शाया जा सकता है:

संख्या रेखा की संरचना

संख्या रेखा:

• एक लम्बी सीधी रेखा होती है जो बाएँ और दाएँ दिशाओं में विस्तारित होती है।
• यह रेखा असीमित होती है, और इसके दोनों सिरों पर पूर्णांकों की संख्या बढ़ती जाती है।

शून्य (0):

• संख्या रेखा का मध्य बिंदु होता है। शून्य के दाएँ दिशा में सकारात्मक पूर्णांक और बाएँ दिशा में नकारात्मक पूर्णांक होते हैं।

सकारात्मक पूर्णांक:

• शून्य के दाएँ दिशा में होते हैं।
• संख्या रेखा पर, ये संख्याएँ क्रम में होती हैं: 1, 2, 3, 4, 5, …

नकारात्मक पूर्णांक:

• शून्य के बाएँ दिशा में होते हैं।
• संख्या रेखा पर, ये संख्याएँ क्रम में होती हैं: -1, -2, -3, -4, -5, …

संख्या रेखा पर पूर्णांकों का प्रदर्शन

सकारात्मक पूर्णांक:

• सकारात्मक पूर्णांक शून्य के दाएँ दिशा में होते हैं। उदाहरण के लिए, 1 को शून्य के दाएँ एक यूनिट की दूरी पर अंकित किया जाएगा, 2 को एक और यूनिट की दूरी पर, और इसी प्रकार।

नकारात्मक पूर्णांक:

• नकारात्मक पूर्णांक शून्य के बाएँ दिशा में होते हैं। उदाहरण के लिए, -1 को शून्य के बाएँ एक यूनिट की दूरी पर अंकित किया जाएगा, -2 को एक और यूनिट की दूरी पर, और इसी प्रकार।

उदाहरण के लिए एक संख्या रेखा

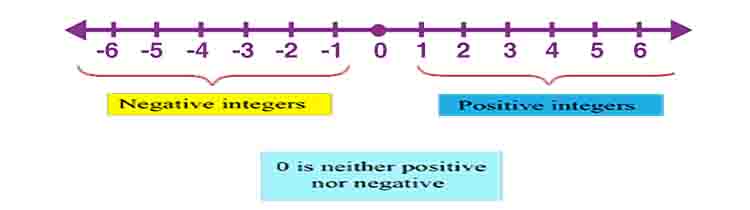
• सकारात्मक पूर्णांक: दाएँ की ओर अंकित होते हैं: 1, 2, 3, 4, आदि।
• नकारात्मक पूर्णांक: बाएँ की ओर अंकित होते हैं: -1, -2, -3, -4, आदि।
• शून्य: मध्य बिंदु पर होता है और अन्य पूर्णांकों के बीच में होता है।

संख्या रेखा का उपयोग

1. गणना: जोड़ और घटाव की गणनाओं को दृश्य रूप से समझने के लिए उपयोगी।
2. माप: पूर्णांकों के बीच की दूरी को दर्शाने के लिए।
3. तुलना: संख्याओं की तुलना करने और उनके क्रम को समझने के लिए।

संख्या रेखा एक महत्वपूर्ण टूल है जो गणितीय अवधारणाओं को स्पष्ट करने और संख्याओं के आपसी संबंधों को समझने में मदद करता है।

पूर्णांकों की गुणधर्म

• अवयवता (Commutative Property): जोड़ और गुणा करने पर, पूर्णांकों के क्रम का प्रभाव नहीं पड़ता। उदाहरण के लिए, a + b = b + a और a x b = b x a।
• संघटन (Associative Property): जोड़ और गुणा में पूर्णांकों का संघटन भी महत्वपूर्ण है। उदाहरण के लिए, (a+b) +c = a+ (b+c) और (a×b) × c = a × (b×c)।
• नैतिकता (Distributive Property): गुणा जोड़ के ऊपर वितरित होता है। उदाहरण के लिए, a× (b+c) = (a×b) + (a×c)।

पूर्णांकों का उपयोग

• गणितीय अभ्यस्तता: गणितीय समीकरणों और विषमताओं को हल करने में।
• सांख्यिकी: डेटा विश्लेषण और सांख्यिकी में संख्याओं की गणना।
• कंप्यूटर विज्ञान: कंप्यूटर प्रोग्रामिंग में डेटा को स्टोर और प्रोसेस करने के लिए।

संख्यात्मक अनुक्रम

पूर्णांकों को एक संख्या रेखा पर दर्शाया जा सकता है, जिसमें शून्य मध्य बिंदु होता है और सकारात्मक पूर्णांक दाएं और नकारात्मक पूर्णांक बाएं होते हैं।

पूर्णांकों का क्रम और अभ्यस्तता:

• क्रम (Order): पूर्णांकों की संख्या रेखा पर क्रम को दर्शाती है। शून्य के दाएं दिशा में सकारात्मक पूर्णांक होते हैं और बाएं दिशा में नकारात्मक पूर्णांक होते हैं।
• मामले और अनुपात (Comparisons and Ratios): पूर्णांकों की तुलना की जा सकती है (जैसे a>b या a<b)। अनुपात और प्रतिशत गणनाओं में भी पूर्णांकों का उपयोग किया जाता है।

पूर्णांकों का सेट और नॉटेशन:

• नोटेशन: पूर्णांकों को आमतौर पर Z से दर्शाया जाता है, जिसमें Z⁺ सकारात्मक पूर्णांकों के लिए, Z⁻ नकारात्मक पूर्णांकों के लिए, और Z⁰ शून्य के लिए होता है।
• संपूर्ण संख्या (Whole Numbers): ये शून्य और सकारात्मक पूर्णांकों का सेट होता है। उदाहरण: 0, 1, 2, 3, …

महत्वपूर्ण पूर्णांक संक्रियाएँ

• जोड़ना: दो पूर्णांकों का जोड़ एक पूर्णांक होता है।
• घटाना: दो पूर्णांकों का घटाव भी एक पूर्णांक देता है।
• गुणा: दो पूर्णांकों का गुणा भी एक पूर्णांक होता है।
• विभाजन: एक पूर्णांक को दूसरे से विभाजित करने पर, प्राप्त संख्या पूर्णांक हो सकती है या नहीं, यह पूर्णांकों की विशिष्टता पर निर्भर करता है।

पूर्णांकों का जोड़ना

समान चिह्न वाले दो पूर्णांकों को जोड़ते समय, उनके निरपेक्ष मान जोड़ें, और योगफल को संख्याओं के साथ दिए गए चिह्न के साथ लिखें।

उदाहरण के लिए,

(+4) + (+7) = +11

(-6) + (-4) = -10

भिन्न चिह्नों वाले दो पूर्णांकों को जोड़ते समय, निरपेक्ष मान घटाएँ, तथा अंतर को उस संख्या के चिह्न के साथ लिखें जिसका निरपेक्ष मान सबसे बड़ा हो।

उदाहरण के लिए,

(-4) + (+2) = -2

(+6) + (-4) = +2.

पूर्णांकों का घटाना

दो पूर्णांकों को घटाते समय, घटाई जा रही दूसरी संख्या का चिह्न बदल दें और योग के नियमों का पालन करें।

उदाहरण के लिए,

(-7) – (+4) = (-7) + (-4) = -11

(+8) – (+3) = (+8) + (-3) = +5

पूर्णांकों का गुणा

दो पूर्णांक संख्याओं को गुणा करते समय नियम सरल है।

• यदि दोनों पूर्णांकों का चिह्न समान हो, तो परिणाम धनात्मक होगा।
• यदि पूर्णांकों के चिह्न भिन्न हों, तो परिणाम ऋणात्मक होगा।

उदाहरण के लिए,

• (+2) x (+3) = +6
• (+3) x (-4) = – 12

इस प्रकार, हम नीचे दी गई तालिका में उदाहरणों के साथ दो पूर्णांकों के गुणन को संक्षेप में प्रस्तुत कर सकते हैं।

चिह्नों का गुणन	परिणामी चिह्न	उदाहरण
+ × +	+	3 × 4 = 12
+ × –	–	3 × -4 = -12
– × +	–	-3 × 4 = -12
– × –	+	-3 × -4 = 12

पूर्णांकों का विभाजन

पूर्णांकों को विभाजित करने का नियम गुणन के समान है।

• यदि दोनों पूर्णांकों का चिह्न समान हो, तो परिणाम धनात्मक होगा।
• यदि पूर्णांकों के चिह्न भिन्न हों, तो परिणाम ऋणात्मक होगा।

उसी प्रकार

• (+6) ÷ (+2) = +3
• (-16) ÷ (+4) = -4

संकेतों का प्रभाग	परिणामी संकेत	उदाहरण
+ ÷ +	+	15 ÷ 3 = 5
+ ÷ –	–	15 ÷ -3 = -5
– ÷ +	–	-15 ÷ 3 = -5
– ÷ –	+	-15 ÷ -3 = 5

पूर्णांक गणितीय प्रक्रियाओं और वास्तविक जीवन की समस्याओं को हल करने में बुनियादी भूमिका निभाते हैं।

पूर्णांकों के उदाहरण

पूर्णांकों के सवाल और उनके हल देने से पूर्णांकों की समझ को बेहतर किया जा सकता है। यहाँ कुछ उदाहरण प्रश्न और उनके हल दिए गए हैं:

जोड़ (Addition):

प्रश्न: 7 + (-3) = ?

हल:

• यहाँ, हम एक सकारात्मक पूर्णांक 7 और एक नकारात्मक पूर्णांक -3 को जोड़ रहे हैं।
• यह मानते हुए कि दोनों पूर्णांकों के संकेत अलग-अलग हैं, हम उनकी आपस की दूरी निकालते हैं: 7 – 3 = 4
• चूंकि सकारात्मक पूर्णांक बड़ा है, परिणाम भी सकारात्मक होगा।
• उत्तर: 4

घटाव (Subtraction)

प्रश्न: -5 – 8 = ?

हल:

• यहाँ, हम -5 से 8 को घटा रहे हैं।
• नकारात्मक पूर्णांक से नकारात्मक पूर्णांक को घटाते समय, हम दोनों के मान को जोड़ते हैं और चूंकि दोनों नकारात्मक हैं, परिणाम भी नकारात्मक होगा: -5 – 8 = -13
• उत्तर: -13

गुणा (Multiplication)

प्रश्न: -4 x 6 = ?

हल:

• यहाँ, हम -4 को 6 से गुणा कर रहे हैं।
• एक नकारात्मक पूर्णांक और एक सकारात्मक पूर्णांक का गुणा नकारात्मक होता है।
• गुणा के परिणाम में पूर्णांकों के मान को गुणा करें: -4 x 6 = – 24
• चूंकि एक पूर्णांक नकारात्मक है, परिणाम भी नकारात्मक होगा।
• उत्तर: -24

विभाजन (Division)

प्रश्न: 12/4 = ?

हल:

• यहाँ, हम -12 को 4 से विभाजित कर रहे हैं।
• एक नकारात्मक पूर्णांक को सकारात्मक पूर्णांक से विभाजित करते समय, परिणाम नकारात्मक होता है।
• विभाजन का परिणाम निकालें: -12/4 = 3)
• चूंकि नकारात्मक पूर्णांक को विभाजित किया जा रहा है, परिणाम नकारात्मक होगा।
• उत्तर: -3

पूर्णांकों के अनुपात (Ratio)

प्रश्न: दो पूर्णांकों 9 और -3 का अनुपात क्या होगा?

हल:

• अनुपात निकालने के लिए, हम दोनों पूर्णांकों को एक-दूसरे से विभाजित करते हैं: 9/-3 = -3
• उत्तर: -3

पूर्णांक की तुलना (Comparison)

प्रश्न: कौन सा बड़ा है: -7 या 5?

हल:

• पूर्णांकों की तुलना करते समय, सकारात्मक पूर्णांक हमेशा नकारात्मक पूर्णांक से बड़ा होता है।
• इसलिए, 5 जो है वो -7 से बड़ा है।
• उत्तर: 5 बड़ा है।

पूर्णांकों का जोड़ और गुणा

प्रश्न: (4 + (-6) x (-2) = ?

हल:

• पहले जोड़ को हल करें: 4 + (-6) = -2
• फिर, गुणा करें: -2 x (-2) = 4 (दो नकारात्मक पूर्णांकों का गुणा सकारात्मक होता है)
• उत्तर: 4

ये उदाहरण पूर्णांकों के विभिन्न गणितीय ऑपरेशनों को समझने में मदद करेंगे और विभिन्न प्रकार की समस्याओं को हल करने के लिए एक ठोस आधार प्रदान करेंगे।

Maths – KnowledgeSthali

---

इन्हें भी देखें –

• लाभ और हानि
• भारतीय संविधान सभा और संविधान निर्माण
• भारत का संवैधानिक इतिहास | ब्रिटिश अधिनियमों और सुधारों का योगदान
• प्राकृतिक संख्या
• Programming Language