भिन्न | Fraction

भिन्न (Fraction) एक गणितीय अवधारणा है जिसका उपयोग संख्याओं को भागों में विभाजित करने के लिए किया जाता है। यह दो पूर्णांकों के अनुपात को व्यक्त करता है और सामान्यतः a/b के रूप में लिखा जाता है, जहाँ ( a ) अनुपात के अंश (numerator) को और ( b ) हर (denominator) को दर्शाता है। अंश ( a ) उस संख्या को दिखाता है जो भाग लिया जाता है, और हर ( b ) कुल भागों की संख्या को दर्शाता है।

भिन्न गणितीय गणनाओं में महत्वपूर्ण भूमिका निभाते हैं, जैसे जोड़, घटाव, गुणा और भाग। इन्हें सरल भिन्नों (जिनका अंश और हर पूर्णांक होते हैं और कोई सामान्य भाजक नहीं होता) और मिश्रित भिन्नों (जिनमें एक पूर्णांक और एक साधारण भिन्न होता है) में विभाजित किया जा सकता है।

भिन्नों का उपयोग दैनिक जीवन में भी होता है, जैसे खाना पकाने में, समय की गणना में, और विविध अनुपातों की गणना में। यह मापन और विविध गणनाओं में विभाजन की एक आधारभूत विधि प्रदान करता है। गणितीय समस्याओं और उनके समाधानों में भिन्नों का सही उपयोग करना महत्वपूर्ण है, क्योंकि यह संख्याओं के बीच सटीक अनुपात और संबंध को व्यक्त करता है।

भिन्नों की एक और महत्वपूर्ण विशेषता उनकी संकुचित (simplified) और विस्तारित (expanded) रूप में अभिव्यक्ति है। संकुचित रूप में भिन्नों को तब दर्शाया जाता है जब अंश और हर का कोई भी सामान्य भाजक न हो, जबकि विस्तारित रूप में भिन्नों को एक या अधिक सामान्य भाजकों के साथ लिखा जा सकता है।

भिन्न की परिभाषा | Definition of Fraction

गणित में “भिन्न” अथवा “फ्रैक्शन” एक ऐसा संख्यात्मक मूल्य है जो किसी पूर्णांक के भाग को दर्शाता है। यह दो संख्याओं के रूप में लिखा जाता है: एक अंश (numerator) और एक हर (denominator), जो अंश के नीचे होता है। उदाहरण के लिए, 3/4​ एक भिन्न है, जहाँ 3 अंश है और 4 हर है।

• परिभाषा 1: भिन्न एक संख्यात्मक मान को दर्शाता है, जो एक संपूर्ण के भागों को परिभाषित करता है। 
• परिभाषा 2: भिन्न वह संख्या है जो किसी पूर्ण के एक भाग को दर्शाती है।

सामान्यतः अंश किसी सम्पूर्ण वस्तु की किसी भी मात्रा का भाग हो सकता है तथा सम्पूर्ण कोई भी विशिष्ट वस्तु या मूल्य हो सकता है।

भिन्नों के भाग

भिन्नों में दो भाग होते हैं, अंश और हर।

• अंश: यह भिन्न का ऊपरी भाग है, जो भिन्न के खंडों को दर्शाता है
• हर: यह निचला या निचला भाग है जो भिन्न को विभाजित करने वाले कुल भागों को दर्शाता है।

उदाहरण: यदि 3/4 एक भिन्न है, तो 3 अंश है और 4 हर है।

भिन्नों के गुण

वास्तविक संख्याओं और पूर्ण संख्याओं की तरह, भिन्नात्मक संख्या में भी कुछ महत्वपूर्ण गुण होते हैं। वे हैं:

• विनिमेय और साहचर्य गुण भिन्नात्मक जोड़ और गुणन के लिए सत्य हैं
• भिन्नात्मक योग का पहचान तत्व 0 है, और भिन्नात्मक गुणन का पहचान तत्व 1 है
• a/b का गुणात्मक व्युत्क्रम b/a है, जहाँ a और b शून्येतर तत्व होने चाहिए
• भिन्नात्मक संख्याएँ योग पर गुणन के वितरण गुण का पालन करती हैं

भिन्नों के प्रकार

भिन्नों के कई प्रकार होते हैं, जिन्हें उनकी संरचना और विशेषताओं के आधार पर वर्गीकृत किया जा सकता है। आइए इन भिन्नों के विभिन्न प्रकारों को विस्तार से समझते हैं:

1. समान भिन्न (Proper Fractions)

• इन भिन्नों में अंश (Numerator) हर (Denominator) से छोटा होता है।
• उदाहरण: 3/4, 5/8, 7/10.

2. असमान भिन्न (Improper Fractions)

• इन भिन्नों में अंश हर के बराबर या उससे बड़ा होता है।
• उदाहरण: 5/3, 9/4, 9/7.

3. मिश्रित भिन्न (Mixed Fractions)

• मिश्रित भिन्न एक पूर्णांक और एक समान भिन्न का संयोजन होता है।
• उदाहरण: 2(1/2), 5(3/4), 7(6/8).
• इन्हें असमान भिन्नों में भी बदला जा सकता है: 2(1/2) = 5/2 , 5(3/4) = ​23/4.

4. समान हर वाले भिन्न (Like Fractions)

• समान हर वाले भिन्न वे होते हैं जिनके हर समान होते हैं।
• उदाहरण: 2/7, 5/7, 3/7

5. विषम हर वाले भिन्न (Unlike Fractions)

• विषम हर वाले भिन्न वे होते हैं जिनके हर अलग-अलग होते हैं।
• उदाहरण: 2/5, 6/7, 7/9.

6. समान भिन्न (Equivalent Fractions)

• समान भिन्न वे होते हैं जो संख्यात्मक रूप से समान होते हैं, भले ही उनके अंश और हर अलग-अलग हों।
• उदाहरण: 1/2 = 2/4 = 4/8.

7. सरल भिन्न (Simplified Fractions)

• वे भिन्न जिन्हें उनके अंश 6/8 को 3/4 में सरल रूप में लिखा जा सकता है।

8. शुद्ध भिन्न (Proper and Improper Fractions as Pure Fractions)

• शुद्ध भिन्न समान और असमान भिन्नों का एक और नाम होता है।

उदाहरण:

• समान भिन्न (Proper Fractions): 3/4.
• असमान भिन्न (Improper Fractions): 9/5.
• मिश्रित भिन्न (Mixed Fractions): 1(2/3).
• समान हर वाले भिन्न (Like Fractions): 2/7, 5/7.
• विषम हर वाले भिन्न (Unlike Fractions): 2/5, 5/8.
• समान भिन्न (Equivalent Fractions): 1/2 = 2/4 = 4/8.
• सरल भिन्न (Simplified Fractions): 6/8 = 3/4.

भिन्नों के प्रकारों का उपयोग

भिन्नों के इन विभिन्न प्रकारों का उपयोग गणितीय समस्याओं को हल करने में किया जाता है। इनका सही प्रकार से समझना और प्रयोग करना आवश्यक है।

इकाई अंश | Unit fraction

किसी भिन्न को इकाई भिन्न तब कहते हैं जब उसका अंश 1 के बराबर हो। 

• पूरे का आधा = 1/2
• सम्पूर्ण का एक तिहाई = 1/3
• सम्पूर्ण का एक-चौथाई = 1/4
• पूर्ण का पाँचवाँ भाग = 1/5

संख्या रेखा पर भिन्न

संख्या रेखा पर भिन्नों को दर्शाना एक महत्वपूर्ण गणितीय अवधारणा है। यह विधि हमें भिन्नों के मान को दृश्य रूप में समझने में मदद करती है और भिन्नों के बीच संबंधों को स्पष्ट करती है।

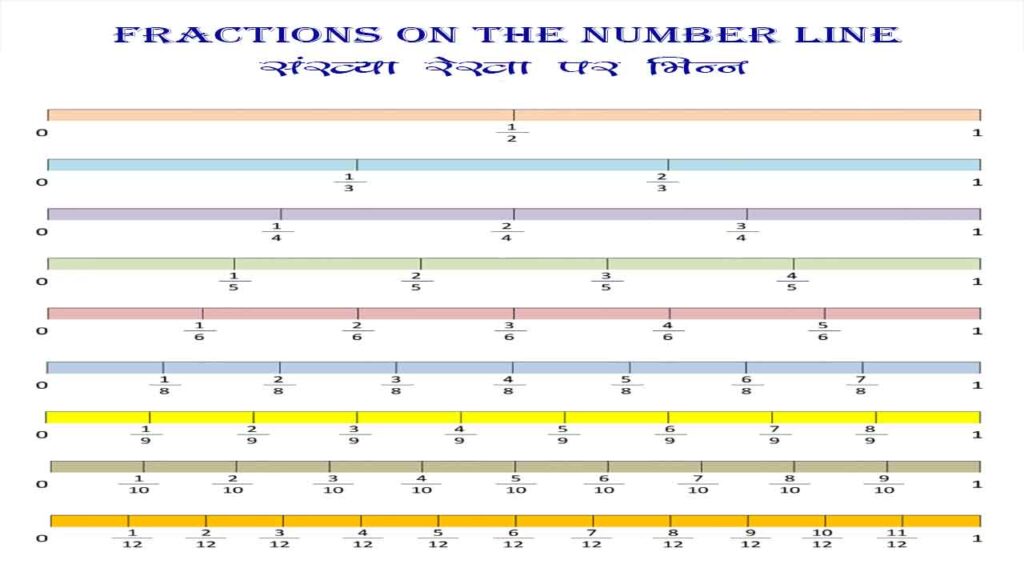
संख्या रेखा पर भिन्नों को दर्शाने के चरण

1. संख्या रेखा खींचें:

• एक सीधी रेखा खींचें और उसे बाएँ से दाएँ तक बढ़ाएँ।
• रेखा पर अंक चिह्नित करें जैसे (0, 1, 2, 3,) आदि।

1. भिन्न के हर को निर्धारित करें:

• हर (Denominator) बताता है कि रेखा को कितने समान भागों में विभाजित करना है।
• उदाहरण: 1/4 के लिए, रेखा को 4 समान भागों में विभाजित करें।

1. भिन्न के अंश को निर्धारित करें:

• अंश (Numerator) बताता है कि हमें कितने भागों की गिनती करनी है।
• उदाहरण: 3/4 के लिए, 0 से लेकर 3 भाग गिनें।

1. भिन्न को चिह्नित करें:

• अंश के अनुसार भागों को गिनते हुए बिंदु लगाएँ।

उदाहरण:

1/2 को संख्या रेखा पर दर्शाना

1. संख्या रेखा खींचें: 0) और 1 के बीच।
2. हर निर्धारित करें: हर 2 है, तो 0 और 1 के बीच रेखा को 2 बराबर भागों में विभाजित करें।
3. अंश निर्धारित करें: अंश 1 है, तो 0 से 1 के बीच एक भाग गिनें।
4. भिन्न चिह्नित करें: 0 से एक भाग गिनते हुए बिंदु लगाएँ, जो 0.5 या 1/2 पर होगा।

3/4 को संख्या रेखा पर दर्शाना

1. संख्या रेखा खींचें: 0 और 1 के बीच।
2. हर निर्धारित करें: हर 4 है, तो 0 और 1 के बीच रेखा को 4 बराबर भागों में विभाजित करें।
3. अंश निर्धारित करें: अंश 3 है, तो 0 से 3 भाग गिनें।
4. भिन्न चिह्नित करें: 0 से तीन भाग गिनते हुए बिंदु लगाएँ, जो 0.75 या 3/4 पर होगा।

कुछ और उदाहरण

2/3 को संख्या रेखा पर दर्शाना

1. संख्या रेखा खींचें: 0 और 1 के बीच।
2. हर निर्धारित करें: हर 3 है, तो 0 और 1 के बीच रेखा को 3 बराबर भागों में विभाजित करें।
3. अंश निर्धारित करें: अंश 2 है, तो 0 से 2 भाग गिनें।
4. भिन्न चिह्नित करें: 0 से दो भाग गिनते हुए बिंदु लगाएँ, जो 2/3 पर होगा।

संक्षेप में

संख्या रेखा पर भिन्नों को दर्शाने से हमें भिन्नों के मान और उनके बीच के अंतर को स्पष्ट रूप से समझने में मदद मिलती है। यह विधि गणित के शिक्षण और भिन्नों की तुलना करने में बहुत उपयोगी है।

भिन्नों को दशमलव में कैसे बदलें?

भिन्नों को दशमलव (Decimal) में बदलने के लिए आप अंश (Numerator) को हर (Denominator) से भाग (Divide) करते हैं। यह प्रक्रिया सरल होती है और निम्नलिखित चरणों में की जा सकती है:

चरण 1: भिन्न को सामान्य रूप में लिखें

उदाहरण के लिए, 3/4

चरण 2: अंश को हर से भाग दें

3/4 = 3 ÷ 4

चरण 3: भाग की प्रक्रिया करें

यहाँ 3 को 4 से विभाजित करेंगे:

• 4 को 3 में 0 बार जाता है, इसलिए दशमलव बिंदु लगाएं और शून्य जोड़ें।
• 4 को 30 में 7 बार जाता है ( 4 x 7 = 28), शेष बचता है 2।
• 20 में 4 को 5 बार जाता है (4 x 5 = 20), शेष बचता है 0।

इसलिए, 3/4का दशमलव रूप 0.75 है।

कुछ और उदाहरण

उदाहरण 1: 1/2 को दशमलव में बदलें

1/2 = 1 ÷ 2 = 0.5

उदाहरण 2: 5/8 को दशमलव में बदलें

5/8 = 5 ÷ 8 = 0.625

उदाहरण 3: 7/10 को दशमलव में बदलें

7/10 = 7 ÷ 10 = 0.7

पुनरावर्ती दशमलव (Repeating Decimals)

कभी-कभी भिन्नों को दशमलव में बदलने पर दशमलव अंश पुनरावृत्ति (Repeating) करने लगता है। उदाहरण के लिए, 1/3।

उदाहरण: 1/3 को दशमलव में बदलें

1/3 = 1 ÷ 3 = 0.3 bar

यहाँ 3 पुनरावृत्त होता है, इसलिए इसे 0.3 bar लिखा जाता है।

मिश्रित भिन्न (Mixed Fractions) को दशमलव में बदलना

मिश्रित भिन्न को पहले असमान भिन्न में बदलें, फिर उसे दशमलव में बदलें।

उदाहरण: 2(1/4) को दशमलव में बदलें

1. मिश्रित भिन्न को असमान भिन्न में बदलें: 2(1/4) = 9/4
2. असमान भिन्न को दशमलव में बदलें: 9/4 = 9 ÷ 4 = 2.25.

सारांश

भिन्नों को दशमलव में बदलने के लिए अंश को हर से भाग दें और भागफल लिखें। यह विधि हर प्रकार के भिन्नों के लिए काम करती है और गणितीय समस्याओं को हल करने में उपयोगी होती है।

भिन्नों पर हल किये गए उदाहरण

उदाहरण 1:

क्या 12/6 एक भिन्न है?

समाधान:

हाँ, यह एक भिन्न है। इसे अनुचित भिन्न कहते हैं। 

उदाहरण 2:

130.1200 को भिन्न में बदलें।

समाधान:

• यहाँ दशमलव को भिन्नों में बदलने की अवधारणा का उपयोग किया जाएगा
• 130.1200 = 130.1200/10000 
• = 13012/100

उदाहरण 3:

3/5 और 10/15 को जोड़ें।

समाधान:

• 3 /5 + 10/15 
• 5 और 15 का LCM 15 है
• = (9 + 10)/15
• = 19/15

उदाहरण 4:

निम्नलिखित में से कौन सी भिन्न सबसे बड़ी है?

• (a) 29/23
• (b) 29/27
• (c) 29/25
• (d) 29/30

समाधान:

• दिए गए विकल्पों में से सबसे बड़ी भिन्न ज्ञात करने के लिए, पहले भिन्नात्मक मान को दशमलव मान में बदलें।
• (a) 29/23 = 1.261
• (b) 29/27 = 1.074
• (c) 29/25 = 1.16
• (d) 29/30 = 0.967
• इस प्रकार, 29/23 दिए गए विकल्पों में से सबसे बड़ी भिन्न है।
• अतः विकल्प (a) 29/23 सही उत्तर है।

उदाहरण 5: 

भिन्न 15/65 को सरलतम रूप में लिखें।

समाधान:

• दी गई भिन्न: 15/65.
• 15 के गुणनखंड: 1, 3, 5 और 15
• 65 के गुणनखंड: 1, 5, 13 और 65
• अतः 15 और 65 का महत्तम समापवर्तक (Highest Common Factor or Greatest Common Divisor) 5 है।
• अर्थात HCF or GCD (15, 65) = 5.
• अब, दी गई भिन्न (16/65) के अंश और हर दोनों को 5 से भाग देने पर हमें प्राप्त होता है
• 15/65 = (15/5) / (65/5) = 3/13.
• अतः, भिन्न 15/65 का सरलतम रूप 3/13 है।

Maths – KnowledgeSthali

---

इन्हें भी देखें –

• अपरिमेय संख्याएँ | Irrational Numbers
• परिमेय संख्या | Rational Numbers
• प्राकृतिक संख्या | Natural Numbers
• संख्याएँ | Numbers
• पूर्णांक | Integers
• लाभ और हानि | Profit and Loss
• भारतीय संसद | लोक सभा और राज्य सभा | संरचना और कार्य प्रणाली
• भारत के महान्यायवादी, नियंत्रक एवं महालेखा परीक्षक: भूमिका, नियुक्ति और कर्तव्य
• भारत का मंत्रीपरिषद और मंत्रिमंडल: संरचना और कार्यप्रणाली
• भारत के उपराष्ट्रपति: पद, योग्यता, शक्तियाँ और कर्तव्य
• भारतीय संविधान में राष्ट्रपति का प्रावधान और उसके कर्त्तव्य